2.4. RAČUNALNA LOGIKA

Kako je već u jednom od prethodnih poglavlja izloženo, rad digitalnog računala temelji se na DVA definirana fizikalna stanja:

Znači da se elektronički sklopovi, koji u računalu obavljaju razne operacije, ponašaju slično prekidačima, a različitim elektroničkim izvedbama izvršavaju operacije sa stanjima "1" i "0" po zakonima LOGIČKIH PRIJEDLOGA koji mogu biti ISTINITI ili NEISTINITI. Ne mogu istovremeno biti i jedno i drugo.

Osnovu ove grane logike, koja datira još od Aristotela, praktički je obradio i definirao njene simbole matematičar George Boole. Po njemu je ova grana matematike (zakoni istinitosti) nazvana BOOLE-ova ALGEBRA, a bavi se međusobnim odnosima elemenata u skupu i između skupova.

2.4.1. Logika skupova

SKUP je grupa elemenata koji posjeduju barem jednu zajedničku karakteristiku u jednoj jedinstvenoj grupi elemenata (opći skup). To znači da se grupa elemenata može podijeliti u dvije podgrupe - PODSKUPA i to:

     1. Podskup elemenata sa zajedničkim svojstvima ---- npr. 'A'
     2. Podskup elemenata koji ne pripada pod 1. ------- npr. 'non A'

Tu podjelu u skupu jasnije predočava sljedeća slika.

Slika* 2.4.1 Opći skupovi elemenata / Odnosi između skupova.

Podskupovi 'A' i 'non A' su komplementarni, 'A' se predstavlja kao ISTINIT i pridružuje mu se stanje "1", a njemu komplementaran skup 'non A' kao NEISTINIT i pridružuje mu se stanje "0". Oba stanja kao rezultat obrade ne mogu istovremeno postojati. Isto vrijedi za podskupove 'B' i 'non B'. Također se razmatra interakcija između skupova, odnosno međusobni odnos između elemenata različitih skupova.

Operacije koje povezuju navedena stanja u skupu i između pojedinih skupova su:

      1. Operacija NOT - NE (  ) --- negacija postojećeg stanja

      2. Operacija OR - ILI (  ) --- zahtijeva barem jedno (+) istinito
                                      stanje za rezultat "1" pri obradi
      3. Operacija AND - I (  ) ---- zahtijeva sva (×) istinita stanja
                                      za rezultat "1" pri obradi

         4. Operacija NOR - NILI ------------- negacija OR

         5. Operacija NAND - NI -------------- negacija AND

         6. Operacija EXOR - isključivi ILI -- zahtijeva samo jedno
                                               istinito stanje za
                                               rezultat "1" pri obradi

Prve tri operacije su osnovne, a preostale su iz njih izvedene. Rezultati odnosa između skupova i u skupu prikazuju se TABLICAMA ISTINE kako slijedi.

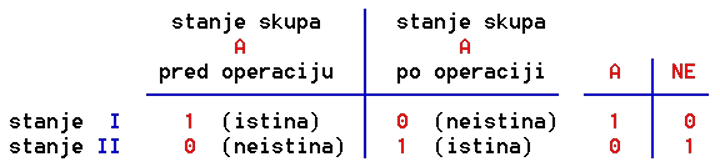
1. Tablica istine operacije NE:

U lijevi stupac tablice upisuju se sva moguća stanja koje skup 'A' može imati, kao i kombinacije svih stanja skupova ako ima više skupova. U desnom stupcu ili stupcima upisuje se stanje koje nastaje kao rezultat izvršene operacije ili operacija nad stanjima prikazanim u lijevom stupcu.

2. Tablica istine operacija ILI, NILI i EXILI (isključivi ILI) izvedenim nad različitim kombinacijama elementa dva skupa.

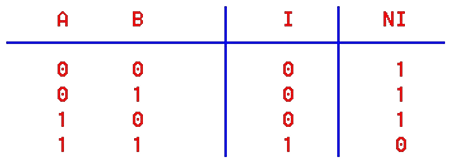
3. Tablica istine operacija I i NI izvedenim nad različitim kombinacijama elementa dva skupa.

Iz tablice proizlazi da neke operacije između skupova odgovaraju operacijama s binarnim brojevima. Ako se "1" i "0" ne koristi za oznaku istine i neistine, već za postojanje i nepostojanje impulsa, posebno konstruirani logički elektronički sklopovi obavljat će logičke operacije s impulsima i omogućiti obavljanje aritmetičkih operacija. Zbog toga se takvi elektronički sklopovi, u pravilu izvedeni u integriranoj tehnici, nazivaju INTEGRIRANI LOGIČKI ELEKTRONIČKI SKLOPOVI.

Prilikom dizajniranja logičkih elektroničkih sklopova, na osnovni dizajn može primijeniti postupak minimizacije logičkih sklopova, čime se dobiva ista potrebna funkcionalnost ali uz manji broj osnovnih logičkih sklopova. Pri tome treba poštovati osnovne zakone Boole-ove algebre koji uređuju odnose među skupovima, a to su:

Zakon komutativnosti : A × B = B × A A + B = B + A Zakon asocijativnosti : (A × B) × C = A × (B × C) (A + B) + C = A + (B + C) Zakon distributivnosti : A × (B + C) = (A × B) + (A × C) A + (B × C) = (A + B) × (A + C) De Morgan-ovi zakoni (teoremi) : _____ _ _ A + B = A × B _____ _ _ A × B = A + B

Znak ' + ' u biti je znak '  ' (a koristi se i znak '  ') - UNIJA, definira skup svih elemenata koji pripadaju barem jednom od skupova A ili B, dakle elementi koji pripadaju bilo kojem od objedinjenih skupova.

Znak ' × ' u biti je znak '  ' (a koristi se i znak '  ') - PRESJEK, definira skup svih elemenata koji pripadaju skupovima A i B, dakle elementi koji istovremeno pripadaju svim promatranim skupovima.

Sukladno navedenom, pošto izlazna stanja logičkih operacija u binarnom sustavu mogu biti "0" ili "1", osnovna PRAVILA POJEDNOSTAVLJIVANJA koja se koriste kod logičkih izraza su:

A = A A × 0 = 0 A + 0 = A A × A = A A + A = A A × 1 = A A + 1 = 1 _ _ A × A = 0 A + A = 1 A × ( A + B ) = A A + ( A × B ) = A _ _ A × ( A + B ) = A × B A + ( A × B ) = A + B

Poštujući ova načela lako je izraditi i minimizirati potrebitu logičku shemu, kojoj su osnovni logički elementi opisani u narednom poglavlju. Što je minimizacija? U osnovi matematički postupak kojim se poštujući navedene zakone veličina zadane logičke funkcije, koja opisuje što će biti na izlazu u ovisnosti o vrijednostima ulaznih varijabli, pojednostavnjuje i smanjuje, te je stoga broj osnovnih logičkih sklopova koje treba uporabiti manji. No, to ostavimo profesionalcima, ali da se zna da je izvedivo.