2.1.2. BINARNI brojevni sustav

Kod dekadnog brojevnog sustava brojimo 'nula, jedan, dva, tri, četiri, pet, šest, sedam, osam, devet, DESET', a 'deset' je u suštini 'nula jedan dalje'. Za binarni brojevni sustav koriste se nazivi dviju znamenki dekadnog sustava; nula (0) i jedan (1). Brojanje u binarnom brojevnom sustavu započinje opisom 'nula, jedan, nula jedan dalje'. Na svaki novi dobiveni binarni broj pribraja se vrijednost "1". Analogno navedenom može se izgraditi binarni sustav brojeva prema primjeru u tablici 2.1.1.

Tablica* 2.1.1 Generiranje binarnog niza cijelih brojeva.

Prema animaciji s prethodne slike, jasno je da su prema binarnom brojevnom sustavu razabiru samo dva stanja: uključeno i isključeno. Izvedbu elektronike koja će pratiti samo ta dva stanja i njihove promjene mnogo je jednostavnije napraviti nego da se istovremeno prati deset različitih stanja, analogno izvedbi prekidača s dva položaja (kao na slici) i prekidača s deset položaja. Stoga ne čudi da se rad digitalnog računala zasniva upravo na binarnom brojevnom sustavu.

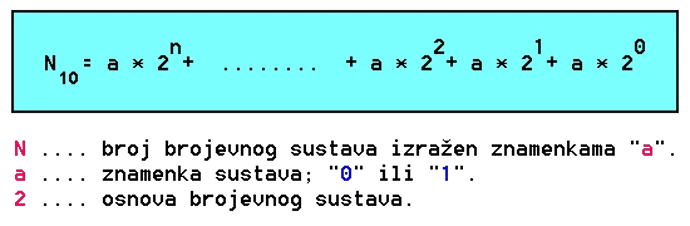
Opći oblik za pretvorbu binarnog broja u dekadni je:

Primjer I

Kolika je dekadna vrijednost binarnog broja 10101101B, prema znaku pod ' I ' sa slike 1.1.3.

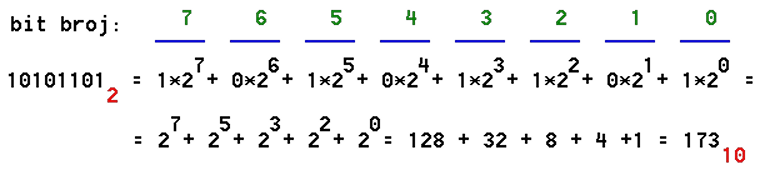Nulti bit, prvi s desna, nosi najmanju težinsku vrijednost (najmanje značajan bit), a težina im raste s desna u lijevo. Vodeći bit, prvi s lijeva, ima najveću težinsku vrijednost (bit najvećeg značaja).

Dakle, pretvorba binarnog broja u dekadni vrlo je jednostavna.

Za binarne brojeve manje od jedan postupak je analogan radnjama za dekadne brojeve npr. za broj 0.101B je:

0.101₂ = 1•2^-1 + 0•2^-2 + 1•2^-3 = 1/2 + 1/9 = 0.61111...₁₀

Primjer II

Kolika je binarna vrijednost dekadnog broja 47 ?

Dijeljenjem dekadnog broja s dva i formiranjem niza od cjelobrojnih ostataka dobije se binarni broj ekvivalentan dekadnom broju po iznosu.

Primjer III

Za brojeve manje od jedan pretvorba se vrši množenjem s dva i formiranjem niza od cjelobrojnog viška izračuna npr. za dekadni broj 0.8215.

Treba voditi računa o samom izgovaranju binarnih brojeva. Ne može se za 101111B reći 'sto jedna tisuća i sto jedanaest', jer sam izgovor podrazumijeva dekadne sadržaje, već treba reći 'jedan, nula, jedan, jedan, jedan, jedan po osnovi dva'.

Primjer IV

Koliko binarnih znamenki ' a ' treba uporabiti da bi se s njima prikazao skup prirodnih brojeva (pozitivni cijeli brojevi) od 0-N?

Broj binarnih kombinacija treba da bude jednak ili veći od dekadnog broja N, te vrijedi:

2 ^a >= N   , iz čega izlazi:

a  >= log₂ ( N )   , ili kraće:

a  >= ld ( N )

Potreban broj binarnih znamenki je prvi veći cijeli broj od izračunatog rezultata. Izračun logaritma po bazi ' 2 ' danas uz moderne kalkulatore nije problem od značaja.

Binarni brojevni sustav je osnova po kojoj će računalo obavljati svoje zadaće na sklopovskoj razini. Prezentiranje numeričkih rezultata u binarnom obliku vrlo je nepregledno i nerazumljivo za korisnika zbog velikog mnoštva znamenki, te se kao međufaza prema dekadnom brojevnom sustavu koriste oktalni i heksadekadni brojevni sustav. Pošto uobičajeni korisnik računala, a vrlo rijetko i profesionalac u informatičkoj struci, u pravilu izravno ne koriste binarni brojevni sustav, opis binarnog brojevnog sustava na ovoj stranici posve je dovoljan da bi se nadalje razumjelo sadržaje koji opisuju na kojim načelima funkcionira računalni sustav.

2.1.3 OKTALNI brojevni sustav

Osim binarnog brojevnog sustava u računalima se koristi i OKTALNI brojevni sustav s bazom 8 i koji koristi nazive i znakove (grafeme) osam znamenki dekadnog brojevnog sustava i to znamenke 0,1,2,3,4,5,6 i 7. Brojevi ovog sustava prikazani su u narednoj tablici:

Tablica 2.1.2 Generiranje dekadnog i oktalnog niza cijelih brojeva.

Opći oblik za pretvorbu oktalnog broja u dekadni je:

Primjer V

Kolika je dekadna vrijednost oktalnog broja 423o?

423₈= 4•8² + 2•8¹ + 3•8⁰ = 256 + 16 + 3 = 275₁₀

Pošto znamenka 7 predstavlja binarnu kombinaciju 111B, dijeljenjem binarnog broja u grupe po tri znamenke lako ga je pretvoriti u oktalni broj:

Kako se danas za prikaz znakova (grafema) koriste uglavnom 8 bit-ne binarne kombinacije, ovaj brojevni sustav imao je svoju primjenu u samim začecima dizajna digitalnog računala kada se je za jedan znak koristilo 7 bit-a. No, širenje na različita tržišta bilo je moguće samo uz dopunu za lokalne grafeme, što je dovelo do primjene 8 bit-nih kombinacija za opis znakova. Gotovo cjelokupna današnja programska potpora u slučaju prikaza binarnih sadržaja dizajnira se da prikazuje skupine od po 4 bit-a, odnosno po dvije skupine za svaki znak prema ASCII kodu, opće prihvaćenim preporukama za kodiranje grafema, te je stoga praktičnija primjena heksadekadnog brojevnog sustava kod kojeg se za svaki znak koriste dvije heksadekadne znamenke. Za praćenje zbivanja na računalu, ili definiranje nekih parametara kao na primjer oznaka boje u GIF formatu slike ili boje pozadine web-stranice, radije se koristi heksadekadni prikaz od binarnog, jer je binarni broj po broju znamenaka velik i kao takav nepregledan.